R pnorm() Function [With Graphical Representation]

by
R pnorm() Method

The pnorm() function in R calculates the cumulative density function (cdf) value of the normal distribution given a specific random variable q, the population mean μ, and the population standard deviation σ.

Visual Representation of pnorm() function

It returns the probability that a normally distributed random variable is less than or equal to a given value.

It provides the probability that a normally distributed random variable will be less than or equal to a specified value.

Syntax

pnorm(q, mean, sd, lower.tail = TRUE, log.p = FALSE)

Parameters

Argument Description
q It is a vector of quantiles.
mean It is a vector of means.
sd It is a vector of standard deviations.
lower.tail It is logical; if TRUE (default), probabilities are otherwise.
log, log.p It is a logical argument.

    Standard Normal Distribution (Default Parameters)

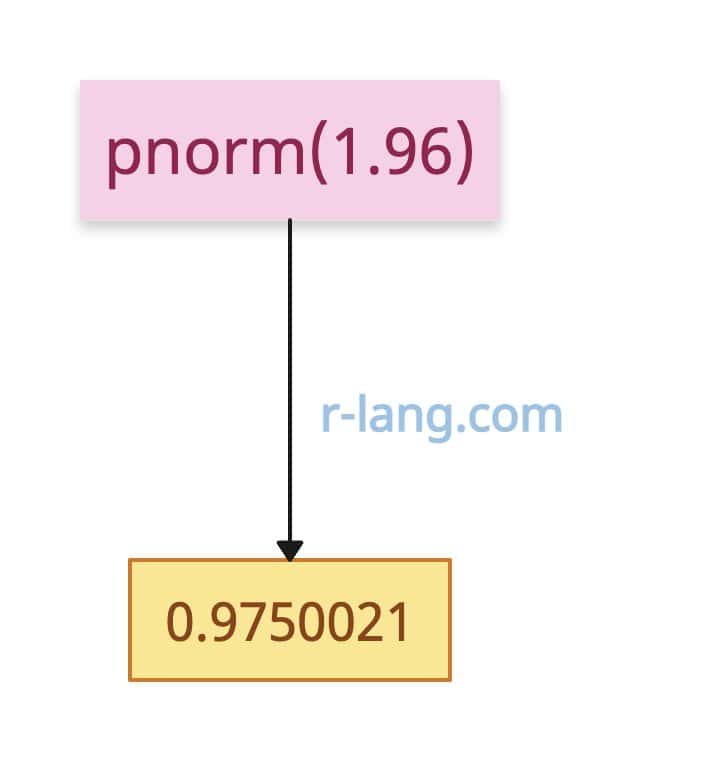
    pnorm()

    pnorm(1.96)

# Output: [1] 0.9750021

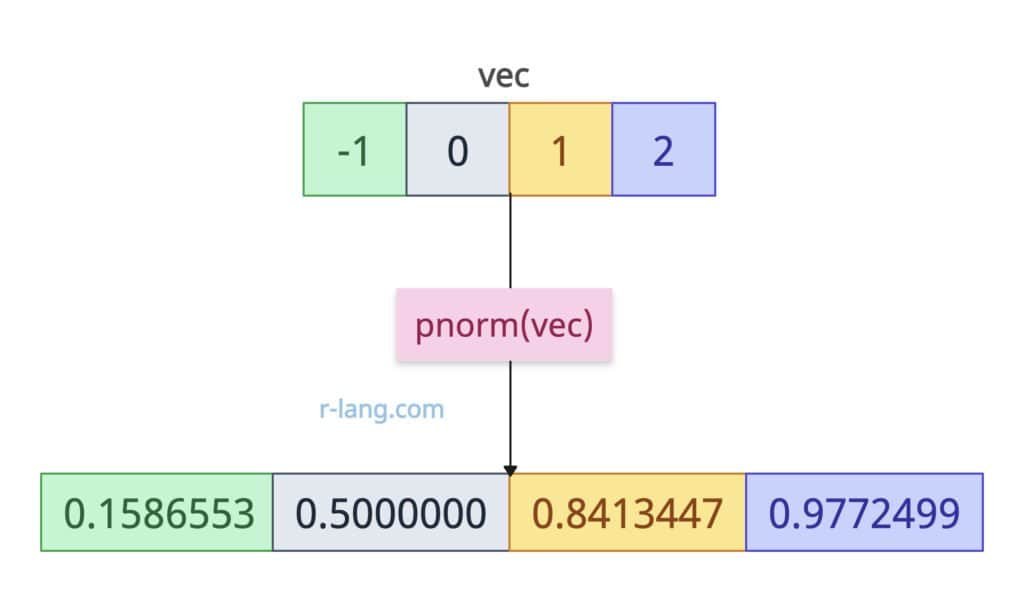
    If we have a vector input, it calculates the pnorm element-wise.

    pnorm() with a vector with multiple elements

    vec <- c(-1, 0, 1, 2)

pnorm(vec)

# Output: [1] 0.1586553 0.5000000 0.8413447 0.9772499

    Extreme input values 

    If the input value is 1000, it will output 1. But if you pass a negative value, what should be the output? Let’s find out.

    pnorm(1000)
# Output: [1] 1 (Overflow-safe; returns 1 for extremely large q)

pnorm(-1000)
# Output: [1] 0

    mean (optional, default = 0)

    It is the mean (μ) of the normal distribution.

    # Standard normal (mean = 0)
pnorm(1, mean = 0)
# Output: [1] 0.8413447

# Custom mean
pnorm(1, mean = 2)
# Output: [1] 0.1586553

pnorm(3, mean = 2)
# Output: [1] 0.8413447

    sd (optional, default = 1)

    It is the standard deviation (σ) of the normal distribution. It must be positive.

    # Standard deviation = 1
pnorm(2, sd = 1)
# Output: [1] 0.9772499

# Standard deviation = 2
pnorm(2, sd = 2)
# Output: [1] 0.8413447

# Standard deviation = 0.5
pnorm(1, sd = 0.5)
# Output: [1] 0.9772499

     

    Non-standard normal distribution

    pnorm(78, mean = 74, sd = 2, lower.tail = FALSE)

# Output: [1] 0.02275013

    Graphical representation

    To visualize this function, we can plot the probability density function (PDF) of the normal distribution and shade the area to the right of x = 78, representing the right-tail probability.

    We will use RStudio to plot the chart and the ggplot2 library. Install if you have not already!

    # Load necessary libraries
library(ggplot2)

# Define parameters
mean_val <- 74
sd_val <- 2

# Create a sequence of x values
x <- seq(68, 80, by = 0.1)

# Calculate the PDF for the x values
y <- pnorm(x, mean = mean_val, sd = sd_val)

# Plot the PDF
p <- ggplot(data.frame(x = x, y = y), aes(x = x, y = y)) +
  geom_line() +
  geom_area(
  data = data.frame(x = x[x >= 78], y = y[x >= 78]),
  aes(x = x, y = y), fill = "skyblue"
 ) +
 geom_vline(aes(xintercept = 78), linetype = "dashed", color = "red") +
 labs(
   title = "Right-tail of Normal Distribution",
   x = "x",
   y = "Density"
 ) +
 theme_minimal()

# Display the plot
print(p)

    Grpahical representation of using the pnorm() function

    Upper-Tail Probabilities

    pnorm(1.96, lower.tail = FALSE)

# Output: [1] 0.0249979

    Log Probability

    log_p <- pnorm(2, log.p = TRUE)

exp(log_p)

# Output: [1] 0.9772499

    Edge cases & errors

    What if the inputs are 0, -inf, inf, or NA? What would the output? Let’s find out.

    # Non-positive sd (error)
pnorm(0, sd = 0)
# Output: [1] 1

# Infinite values
pnorm(-Inf)
# Output: [1] 0.0

pnorm(Inf)
# Output: [1] 1.0

# Missing values
pnorm(NA)
# Output: [1] NA

    That’s all!

    Leave a Comment